[패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 12회차 미션 Programming/Python2020. 11. 13. 16:44
[파이썬을 활용한 데이터 전처리 Level UP- 12 회차 미션 시작]
* 복습
- 통계 분석을 해야 하는 이유에 대해서 그리고, 통계에 대해서 어렵지만 대표 통계량과 산포 통계량에 대해서 배워 볼 수 있었다.
[02. Part 2) 탐색적 데이터 분석 Chapter 09. 변수가 어떻게 생겼나 - 기초 통계 분석 - 04. 분포 통계량]

* 백분위수와 사분위수
- 백분위수 (percentile)는 데이터를 크기 순서대로 오름차순 정렬했을 때, 백분율로 나타낸 특정 위치의 값을 의미

- 사분위 (quantile)는 데이터를 크기 순서대로 오름차순 정렬 했을 때, 4등분한 위치의 값을 의미
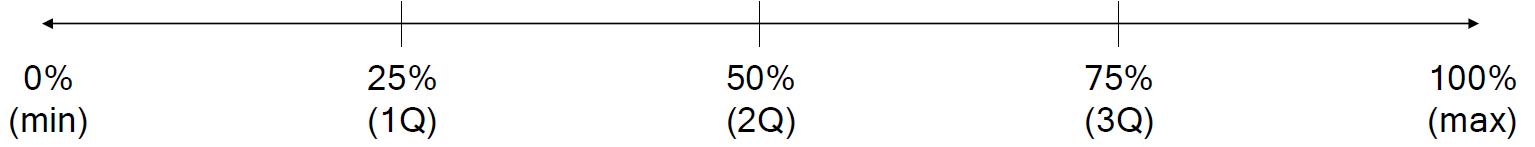
// 1 사분위, 2 사분위 3 사분위
// 일반적으로 많이 보는 것은 백분위수보다는 사분위 수를 더 많이 화룡ㅇ한다.
* 파이썬을 이용한 백분위수와 사분위수 계산

// 동일하지만 q 값을 다르게 각각 넣는다고 생각하면 된다.
// numpy.percentile documentation
numpy.org/doc/stable/reference/generated/numpy.percentile.html
numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)Compute the q-th percentile of the data along the specified axis.
Returns the q-th percentile(s) of the array elements.
Parameters
aarray_like
Input array or object that can be converted to an array.
qarray_like of float
Percentile or sequence of percentiles to compute, which must be between 0 and 100 inclusive.
axis{int, tuple of int, None}, optional
Axis or axes along which the percentiles are computed. The default is to compute the percentile(s) along a flattened version of the array.
Changed in version 1.9.0: A tuple of axes is supported
outndarray, optional
Alternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type (of the output) will be cast if necessary.
overwrite_inputbool, optional
If True, then allow the input array a to be modified by intermediate calculations, to save memory. In this case, the contents of the input a after this function completes is undefined.
interpolation{‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}
This optional parameter specifies the interpolation method to use when the desired percentile lies between two data points i < j:
-
‘linear’: i + (j - i) * fraction, where fraction is the fractional part of the index surrounded by i and j.
-
‘lower’: i.
-
‘higher’: j.
-
‘nearest’: i or j, whichever is nearest.
-
‘midpoint’: (i + j) / 2.
New in version 1.9.0.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original array a.
New in version 1.9.0.
Returns
percentilescalar or ndarray
If q is a single percentile and axis=None, then the result is a scalar. If multiple percentiles are given, first axis of the result corresponds to the percentiles. The other axes are the axes that remain after the reduction of a. If the input contains integers or floats smaller than float64, the output data-type is float64. Otherwise, the output data-type is the same as that of the input. If out is specified, that array is returned instead.
// numpy.quantile documentation
numpy.org/doc/stable/reference/generated/numpy.quantile.html
numpy.quantile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)Compute the q-th quantile of the data along the specified axis.
New in version 1.15.0.
Parameters
aarray_like
Input array or object that can be converted to an array.
qarray_like of float
Quantile or sequence of quantiles to compute, which must be between 0 and 1 inclusive.
axis{int, tuple of int, None}, optional
Axis or axes along which the quantiles are computed. The default is to compute the quantile(s) along a flattened version of the array.
outndarray, optional
Alternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type (of the output) will be cast if necessary.
overwrite_inputbool, optional
If True, then allow the input array a to be modified by intermediate calculations, to save memory. In this case, the contents of the input a after this function completes is undefined.
interpolation{‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}
This optional parameter specifies the interpolation method to use when the desired quantile lies between two data points i < j:
linear: i + (j - i) * fraction, where fraction is the fractional part of the index surrounded by i and j.
lower: i.
higher: j.
nearest: i or j, whichever is nearest.
midpoint: (i + j) / 2.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original array a.
Returns
quantilescalar or ndarray
If q is a single quantile and axis=None, then the result is a scalar. If multiple quantiles are given, first axis of the result corresponds to the quantiles. The other axes are the axes that remain after the reduction of a. If the input contains integers or floats smaller than float64, the output data-type is float64. Otherwise, the output data-type is the same as that of the input. If out is specified, that array is returned instead.
// 이와 함께 참고해볼만한 numpy.median documentation
numpy.org/doc/stable/reference/generated/numpy.median.html#numpy.median
numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)Compute the median along the specified axis.
Returns the median of the array elements.
Parameters
aarray_like
Input array or object that can be converted to an array.
axis{int, sequence of int, None}, optional
Axis or axes along which the medians are computed. The default is to compute the median along a flattened version of the array. A sequence of axes is supported since version 1.9.0.
outndarray, optional
Alternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type (of the output) will be cast if necessary.
overwrite_inputbool, optional
If True, then allow use of memory of input array a for calculations. The input array will be modified by the call to median. This will save memory when you do not need to preserve the contents of the input array. Treat the input as undefined, but it will probably be fully or partially sorted. Default is False. If overwrite_input is True and a is not already an ndarray, an error will be raised.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original arr.
New in version 1.9.0.
Returns
medianndarray
A new array holding the result. If the input contains integers or floats smaller than float64, then the output data-type is np.float64. Otherwise, the data-type of the output is the same as that of the input. If out is specified, that array is returned instead.
* 실습

// 10% 값
* 왜도
- 왜도 (skewness) : 분포의 비대칭도를 나타내는 통계량
- 왜도가 음수면 오른쪾으로 치우친 것을 의미하며, 양수면 왼쪽으로 치우침을 의미한다.
// 0 일때는 정규분포형태라고 볼 수 있다.

- 일반적으로 왜도의 절대값이 1.5 이상이면 치우쳤다고 본다.
* 첨도
- 첨도 (kurtosis) : 데이터의 분포가 얼마나 뾰족한지를 의미한다. 즉, 첨도가 높을수록 이 변수가 좁은 범위에 많은 값들이 몰려있다고 할 수 있다.

* 파이썬을 이용한 왜도와 첨도

// scipy.stats.skew documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.skew.html
scipy.stats.skew(a, axis=0, bias=True, nan_policy='propagate')Compute the sample skewness of a data set.
For normally distributed data, the skewness should be about zero. For unimodal continuous distributions, a skewness value greater than zero means that there is more weight in the right tail of the distribution. The function skewtest can be used to determine if the skewness value is close enough to zero, statistically speaking.
Parameters
andarray
Input array.
axisint or None, optional
Axis along which skewness is calculated. Default is 0. If None, compute over the whole array a.
biasbool, optional
If False, then the calculations are corrected for statistical bias.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
Returns
skewnessndarray
The skewness of values along an axis, returning 0 where all values are equal.
// pandas.Series.skew documentation
pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.skew.html
Series.skew(axis=None, skipna=None, level=None, numeric_only=None, **kwargs)Return unbiased skew over requested axis.
Normalized by N-1.
Parameters
axis{index (0)}
Axis for the function to be applied on.
skipnabool, default True
Exclude NA/null values when computing the result.
levelint or level name, default None
If the axis is a MultiIndex (hierarchical), count along a particular level, collapsing into a scalar.
numeric_onlybool, default None
Include only float, int, boolean columns. If None, will attempt to use everything, then use only numeric data. Not implemented for Series.
**kwargs
Additional keyword arguments to be passed to the function.
Returns
scalar or Series (if level specified)
// scipy.stats.kurtosis documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kurtosis.html
scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy='propagate')Compute the kurtosis (Fisher or Pearson) of a dataset.
Kurtosis is the fourth central moment divided by the square of the variance. If Fisher’s definition is used, then 3.0 is subtracted from the result to give 0.0 for a normal distribution.
If bias is False then the kurtosis is calculated using k statistics to eliminate bias coming from biased moment estimators
Use kurtosistest to see if result is close enough to normal.
Parameters
aarray
Data for which the kurtosis is calculated.
axisint or None, optional
Axis along which the kurtosis is calculated. Default is 0. If None, compute over the whole array a.
fisherbool, optional
If True, Fisher’s definition is used (normal ==> 0.0). If False, Pearson’s definition is used (normal ==> 3.0).
biasbool, optional
If False, then the calculations are corrected for statistical bias.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. ‘propagate’ returns nan, ‘raise’ throws an error, ‘omit’ performs the calculations ignoring nan values. Default is ‘propagate’.
Returns
kurtosisarray
The kurtosis of values along an axis. If all values are equal, return -3 for Fisher’s definition and 0 for Pearson’s definition.
// pandas.Series.kurtosis documentation
pandas.pydata.org/pandas-docs/version/0.23.4/generated/pandas.Series.kurtosis.html
Series.kurtosis(axis=None, skipna=None, level=None, numeric_only=None, **kwargs)Return unbiased kurtosis over requested axis using Fisher’s definition of kurtosis (kurtosis of normal == 0.0). Normalized by N-1
| Parameters: axis : {index (0)} skipna : boolean, default True level : int or level name, default None numeric_only : boolean, default None |
| Returns: kurt : scalar or Series (if level specified) |
* 실습


[02. Part 2) 탐색적 데이터 분석 Chapter 09. 변수가 어떻게 생겼나 - 기초 통계 분석 - 05. 머신러닝에서의 기초 통계 분석]

* 변수 분포 문제 확인
- 머신러닝에서 각 변수를 이해하고, 특별한 분포 문제가 없는지 확인하기 위해 기초 통계 분석을 수행한다.
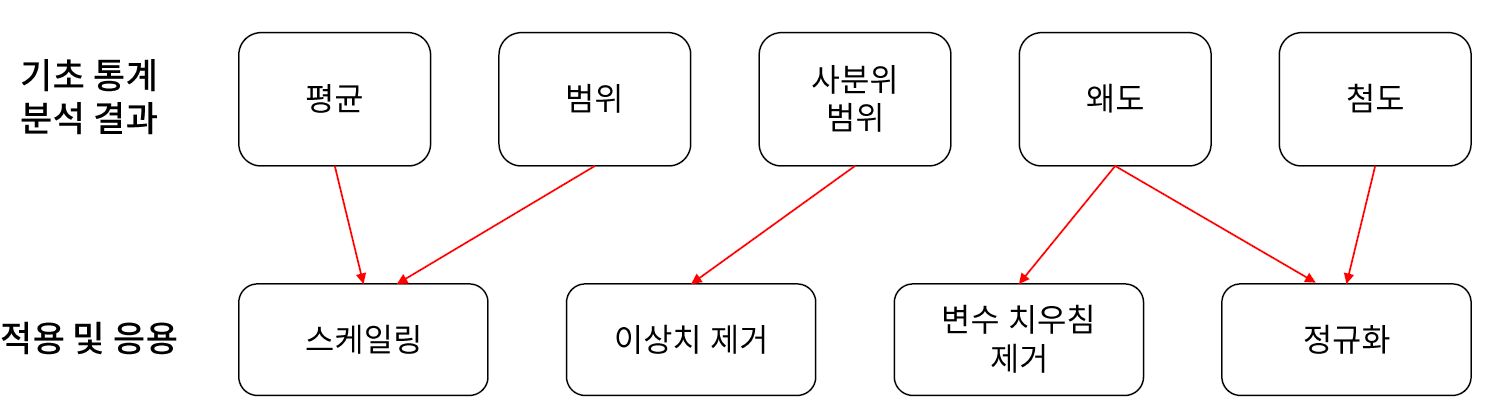
// 평균과 범위로 특징과 스케일링을 알 수 있다. 다시 말해서, 스케일의 편차를 줄인다고 보면 된다.
// 사분위는 이상치 제거를 볼 수가 있다.
// 왜도 같으면.. 1.5보다 크거나 작거나로 치우치는지를 확인해 볼수가 있다... 치우치거나 몰려 있게 되면 정규화를 통해 정의 할 수 있다.
[02. Part 2) 탐색적 데이터 분석 Chapter 10. 둘 사이에는 무슨 관계가 있을까 - 가설 검정과 변수 간 관계 분석 - 01. 영가설과 대립가설, p-value]

* 통계적 가설 검정 개요
- 갖고 있는 샘플을 가지고 모집단의 특성에 대한 가설에 대한 통계적 유의성을 검정하는 일련의 과정
. 수집한 데이터는 매우 특별한 경우를 제외하고는 전부 샘플이며, 모집단은 정확히 알 수 없는 경우가 더 많다.
// 모집단을 정확히 알 수는 없다. 예를 들어 대한민국 남성의 모든 키를 알 수는 없고, 단지 수집한 자료를 가지고 활용할 것이다.
// 보통은 모집단을 알 수 없는 경우가 대부분이다.
. 통계적 유의성 : 어떤 실험 결과 (데이터)가 확률적으로 봐서 단순한 우연이 아니라고 판단될 정도로 의미가 있다.
- 통계적 가설 검정 과정은 다음과 같이 5단계로 구성된다.

* 영 가설과 대립 가설
- 영 가설 (null hypothesis)와 대립 가설(alternative hypothesis)로 구분하여, 가설을 수립해야 한다.
// 영 가설 -> 귀무가설
// 대립 가설 -> 우리가 알고 싶은 대상에 대한 가설
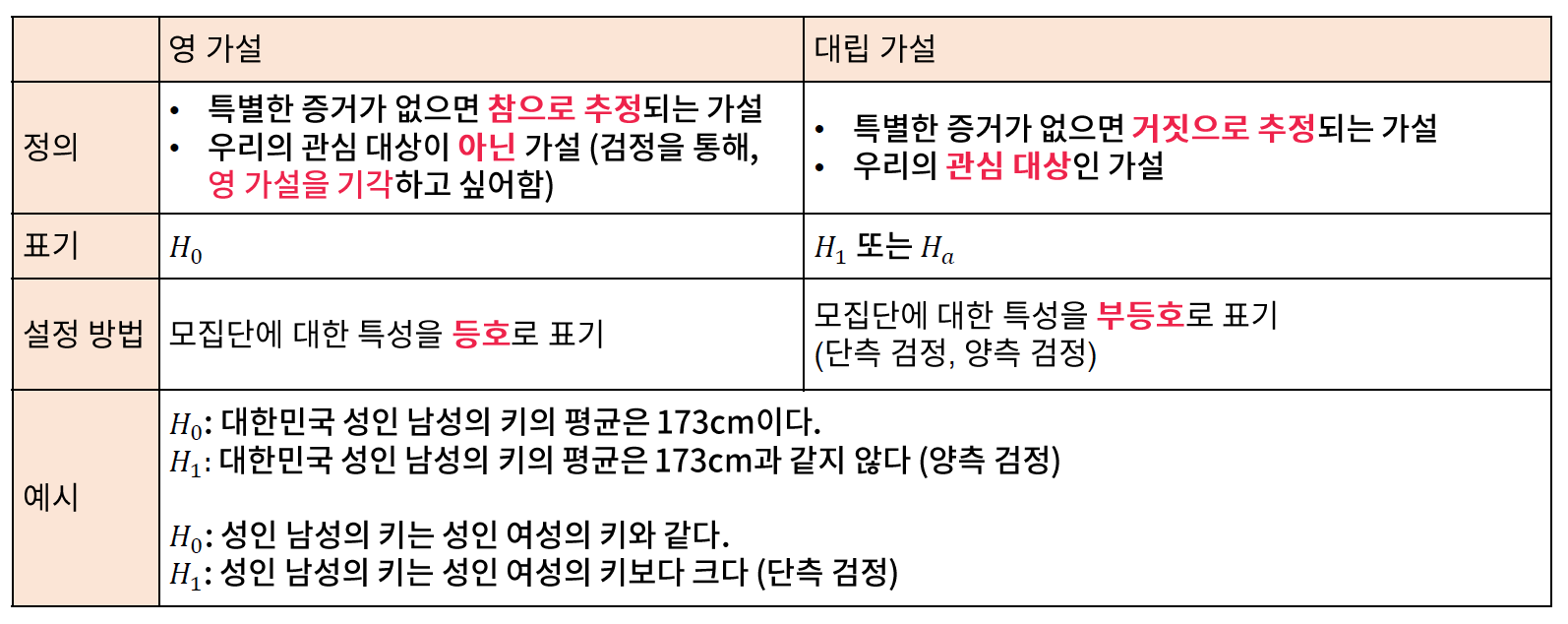
// 영 가설 -> 범죄자는 무죄이다.
// 대립 가설에서는 죄를 찾기 위해서 증거를 수집한다는 예로 들어서 생각해 볼 수 있다.
// 대립 가설 (H 알파..A 가 아니라)
// 양측 검정 -> 키가 크거나 작아도 되므로, 양측 검정
// 단측 검정 -> 성인 남성의 키가 크다라는 검을 검정한다는 의미로 생각하면 된다.
* 오류의 구분
- 가설 검정에서 발생하는 오류는 참을 거짓이라 하는 제 1종 오류 (type 1 Error)와 거짓을 참이라 하는 제 2종 오류로 구분된다.

// 샘플을 가지고 검증하기 때문에 오류가 반드시 난다고 생각하면 된다.
* 유의 확률, p-value
- 유의 확률 p-value : 영 가설이 맞다고 가정할 때 얻은 결과와 다른 결과가 관측될 확률로, 그 값이 작을수록 영 가설을 기각할 근거가 된다.
// 유의 확률, 영 가설, p-value 만 알아도 통계측에서는 90%이상 이해했다고 보면 된다.
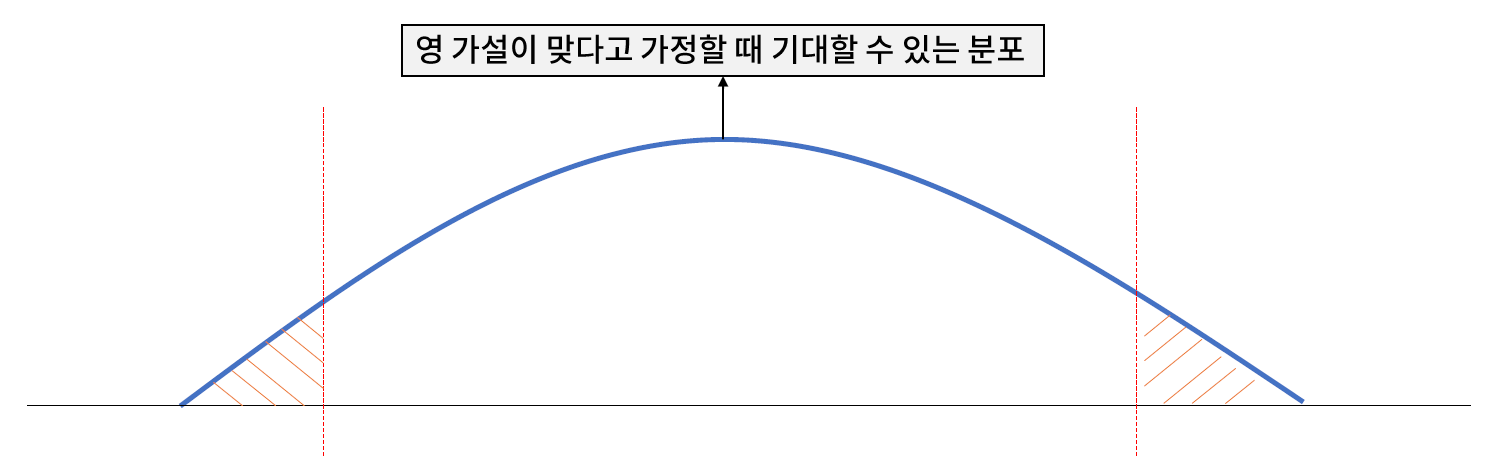
- 보통, p-value 가 0.05 혹은 0.01 미만이면 영 가설을 기각한다.
// 영 가설을 기각한다고 해서 반드시 대립 가설이 참인것은 아니다. 새로운 검증을 해봐야 한다.
* 유의 확률, p-value (예시1)
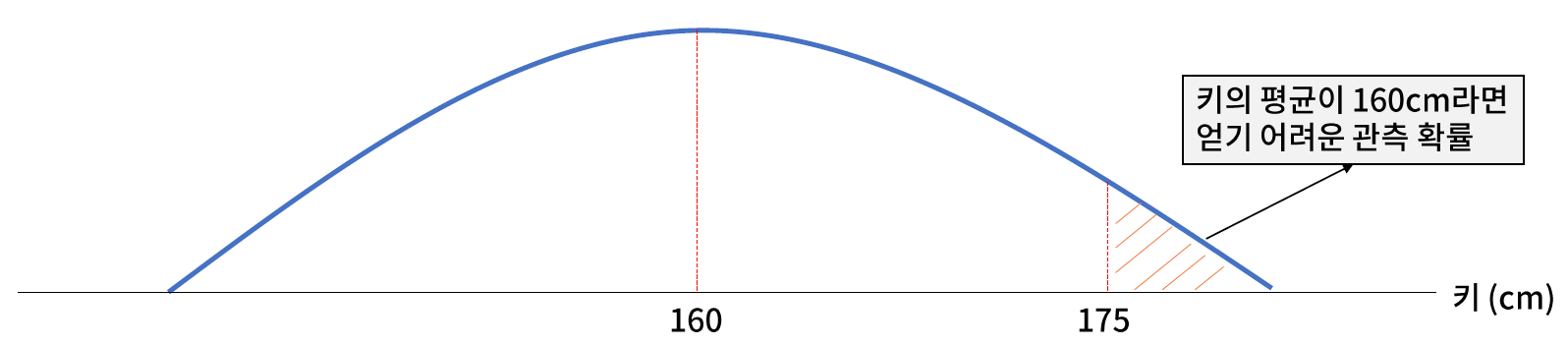
- 영 가설 : 대한민국 성인 남성의 키는 160 cm 일 것이다.
- 대립 가설 : 대한민국 성인 남성의 키는 160 cm 이상일 것이다.
- 관측한 대한민국 성인 남성의 키의 평균은 175 cm, 표준편차는 1cm 이다.
* 유의 확률, p-value (예시2)
- 영 가설 : 대란민국 성인 남성의 키는 여성의 키와 같을 것이다.
- 대립 가설 : 대한민국 성인 남성의 키는 여성의 키보다 작다.

[파이썬을 활용한 데이터 전처리 Level UP-Comment]
- 영가설, 대립가설, p-value 에 대해서 배웠다. p-value
- p-value
The p-value is about the strength of a hypothesis. We build hypothesis based on some statistical model and compare the model's validity using p-value. One way to get the p-value is by using T-test.
This is a two-sided test for the null hypothesis that the expected value (mean) of a sample of independent observations ‘a’ is equal to the given population mean, popmean. Let us consider the following example.
파이썬을 활용한 데이터 전처리 Level UP 올인원 패키지 Online. | 패스트캠퍼스
데이터 분석에 필요한 기초 전처리부터, 데이터의 품질 및 머신러닝 성능 향상을 위한 고급 스킬까지 완전 정복하는 데이터 전처리 트레이닝 온라인 강의입니다.
www.fastcampus.co.kr
'Programming > Python' 카테고리의 다른 글
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 14회차 미션 (0) | 2020.11.15 |
|---|---|
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 13회차 미션 (0) | 2020.11.14 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 11회차 미션 (0) | 2020.11.12 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 10회차 미션 (0) | 2020.11.11 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 9 회차 미션 (0) | 2020.11.10 |


