[패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 13회차 미션 Programming/Python2020. 11. 14. 09:39
[파이썬을 활용한 데이터 전처리 Level UP- 13 회차 미션 시작]
* 복습
- 영가설 : 데이터분석을 하기 위해서 무조건 참이라고 생각되는 가설
- 대립가설 : 영 가설에 포함되지 않는 다른 조건의 가설을 세운다. 영 가설이 틀리다고 해서 무조건 대립 가설이 맞다는 이야기가 아니다.
- p-value 를 통해서 판단한다.
[02. Part 2) 탐색적 데이터 분석 Chapter 10. 둘 사이에는 무슨 관계가 있을까 - 가설 검정과 변수 간 관계 분석 - 02. 단일 표본 t 검정]

* 단일 표본 t-검정 개요
- 목적 : 그룹의 평균이 기준 값과 차이가 있는지를 확인
// 형태를 반드시 확인하는 것이 좋다.
- 영 가설과 대립 가설

// 하나의 영 가설에서도 여러가지 대립 가설이 조건이 생겨 날 수 있다.
- 가설 수립 예시 : 당신이 한 웹 사이트를 운영하고 있는데, 고객이 웹사이트에서 체류하는 평균 시간이 10분인지 아닌지를 알고 싶어 다음과 같이 가설을 수립하였다.

* 단일 표본 t-검정의 선행 조건
- 단일 표본 t - 검정은 해당 변수가 정규 분포를 따라야 수행할 수 있으므로, Komogorov-Smornov 나 Shaprio-Wilk 를 사용한 정규성 검정이 선행되어야 한다.
- 그렇지만 보통 샘플 수가 많을 수록 정규성을 띌 가능성이 높아지므로, 샘플 수가 부족한 경우에만 정규성 검정을 수행한 뒤, 정규성을 띄지 않는다 라고 판단된다면 비모수적 방법인 부호 검정 (sign test)나 윌콕슨 부호 - 순위 검정을 수행해야 한다.
// 수학적으로는 어렵지만 어떤 방법인지정도만 기억해도 무방하다.
* 단일 표본 t - 검정 통계량

// 분자 : 차이가 크면 통계량이 매우 커질수도 있고, 매우 작아질수도 있다. 분자에 있으므로..
// 분모 : s 는 커지면 커질수록 t의 값이 커지고, n 이 커지면 커질수록 t 의 절대값을 키우는 역할을 한다.
- 위에 제시된 통계량을 t분포 상에 위치시키는 방식으로 p-value 를 계산
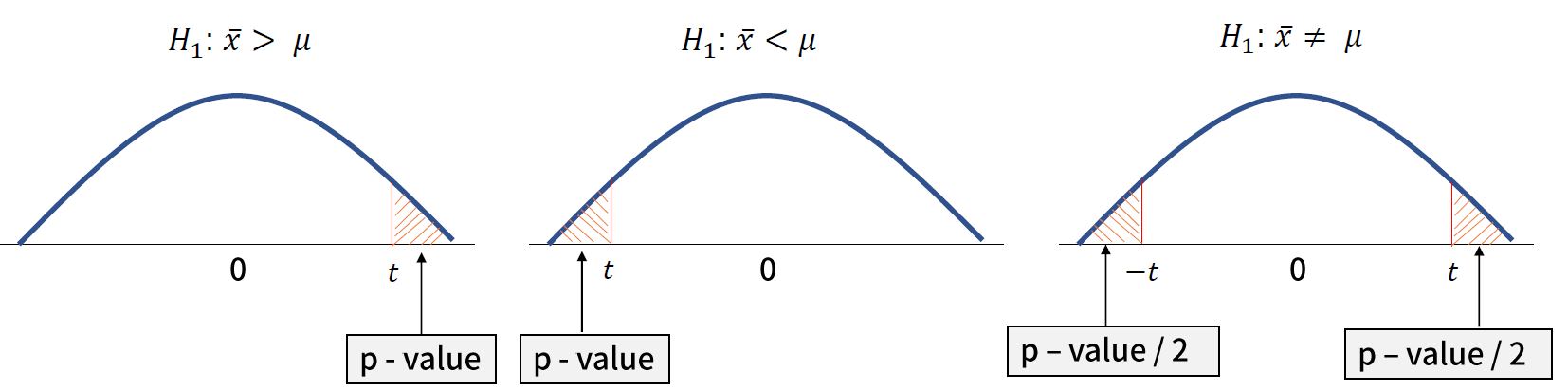
* 정규성 검정 : Kolmogorov-Smornov
- Kolmogorov-Smornov 검정 (이하 KS test) 은 관측한 샘플들이 특정 분포를 따르는지 확인하기 위한 검정 방법이다.
// 정규분포보다는 특정 분포를 검정하기 위한 방법이다.
- KS test 는 특정 분포를 따른다면 나올 것이라 예상되는 값과 실제 값의 차이가 유의한지를 확인하는 방법으로, 해당 특정 분포를 정규 분포로 설정하여 정규성 검정에도 사용한다.
* 파이썬을 이용한 단일 표본 t-검정

// 정규성검증, norm 정규분포. pvalue 를 보기 위한 검정이라고 보면 된다.
// 단일 표본 t - 검정, popmean 에는 기준값이 들어감.
// 윌콕슨 부호 - 순위 검정, 기준값을 설정할 수가 없다. 중위수로 결정된다.
// 평균이 들어가면 평균과 평균의 차이때문에 검증을 할 수 없어서, 중위수 값으로 설정된다.
// scipy.stats.kstest documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kstest.html
scipy.stats.kstest(rvs, cdf, args=(), N=20, alternative='two-sided', mode='auto')Performs the (one sample or two samples) Kolmogorov-Smirnov test for goodness of fit.
The one-sample test performs a test of the distribution F(x) of an observed random variable against a given distribution G(x). Under the null hypothesis, the two distributions are identical, F(x)=G(x). The alternative hypothesis can be either ‘two-sided’ (default), ‘less’ or ‘greater’. The KS test is only valid for continuous distributions. The two-sample test tests whether the two independent samples are drawn from the same continuous distribution.
Parameters
rvsstr, array_like, or callable
If an array, it should be a 1-D array of observations of random variables. If a callable, it should be a function to generate random variables; it is required to have a keyword argument size. If a string, it should be the name of a distribution in scipy.stats, which will be used to generate random variables.
cdfstr, array_like or callable
If array_like, it should be a 1-D array of observations of random variables, and the two-sample test is performed (and rvs must be array_like) If a callable, that callable is used to calculate the cdf. If a string, it should be the name of a distribution in scipy.stats, which will be used as the cdf function.
argstuple, sequence, optional
Distribution parameters, used if rvs or cdf are strings or callables.
Nint, optional
Sample size if rvs is string or callable. Default is 20.
alternative{‘two-sided’, ‘less’, ‘greater’}, optional
Defines the alternative hypothesis. The following options are available (default is ‘two-sided’):
‘two-sided’
‘less’: one-sided, see explanation in Notes
‘greater’: one-sided, see explanation in Notes
mode{‘auto’, ‘exact’, ‘approx’, ‘asymp’}, optional
Defines the distribution used for calculating the p-value. The following options are available (default is ‘auto’):
‘auto’ : selects one of the other options.
‘exact’ : uses the exact distribution of test statistic.
‘approx’ : approximates the two-sided probability with twice the one-sided probability
‘asymp’: uses asymptotic distribution of test statistic
Returns
statisticfloat
KS test statistic, either D, D+ or D-.
pvaluefloat
One-tailed or two-tailed p-value.
// scipy.stats.ttes_1samp documenation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html
scipy.stats.ttest_1samp(a, popmean, axis=0, nan_policy='propagate')Calculate the T-test for the mean of ONE group of scores.
This is a two-sided test for the null hypothesis that the expected value (mean) of a sample of independent observations a is equal to the given population mean, popmean.
Parameters
aarray_like
Sample observation.
popmeanfloat or array_like
Expected value in null hypothesis. If array_like, then it must have the same shape as a excluding the axis dimension.
axisint or None, optional
Axis along which to compute test. If None, compute over the whole array a.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
Returns
statisticfloat or array
t-statistic.
pvaluefloat or array
Two-sided p-value.
// scipy.stats.wilcoxon documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wilcoxon.html
scipy.stats.wilcoxon(x, y=None, zero_method='wilcox', correction=False, alternative='two-sided', mode='auto')Calculate the Wilcoxon signed-rank test.
The Wilcoxon signed-rank test tests the null hypothesis that two related paired samples come from the same distribution. In particular, it tests whether the distribution of the differences x - y is symmetric about zero. It is a non-parametric version of the paired T-test.
Parameters
xarray_like
Either the first set of measurements (in which case y is the second set of measurements), or the differences between two sets of measurements (in which case y is not to be specified.) Must be one-dimensional.
yarray_like, optional
Either the second set of measurements (if x is the first set of measurements), or not specified (if x is the differences between two sets of measurements.) Must be one-dimensional.
zero_method{‘pratt’, ‘wilcox’, ‘zsplit’}, optional
The following options are available (default is ‘wilcox’):
‘pratt’: Includes zero-differences in the ranking process, but drops the ranks of the zeros, see [4], (more conservative).
‘wilcox’: Discards all zero-differences, the default.
‘zsplit’: Includes zero-differences in the ranking process and split the zero rank between positive and negative ones.
correctionbool, optional
If True, apply continuity correction by adjusting the Wilcoxon rank statistic by 0.5 towards the mean value when computing the z-statistic if a normal approximation is used. Default is False.
alternative{“two-sided”, “greater”, “less”}, optional
The alternative hypothesis to be tested, see Notes. Default is “two-sided”.
mode{“auto”, “exact”, “approx”}
Method to calculate the p-value, see Notes. Default is “auto”.
Returns
statisticfloat
If alternative is “two-sided”, the sum of the ranks of the differences above or below zero, whichever is smaller. Otherwise the sum of the ranks of the differences above zero.
pvaluefloat
The p-value for the test depending on alternative and mode.
* 실습
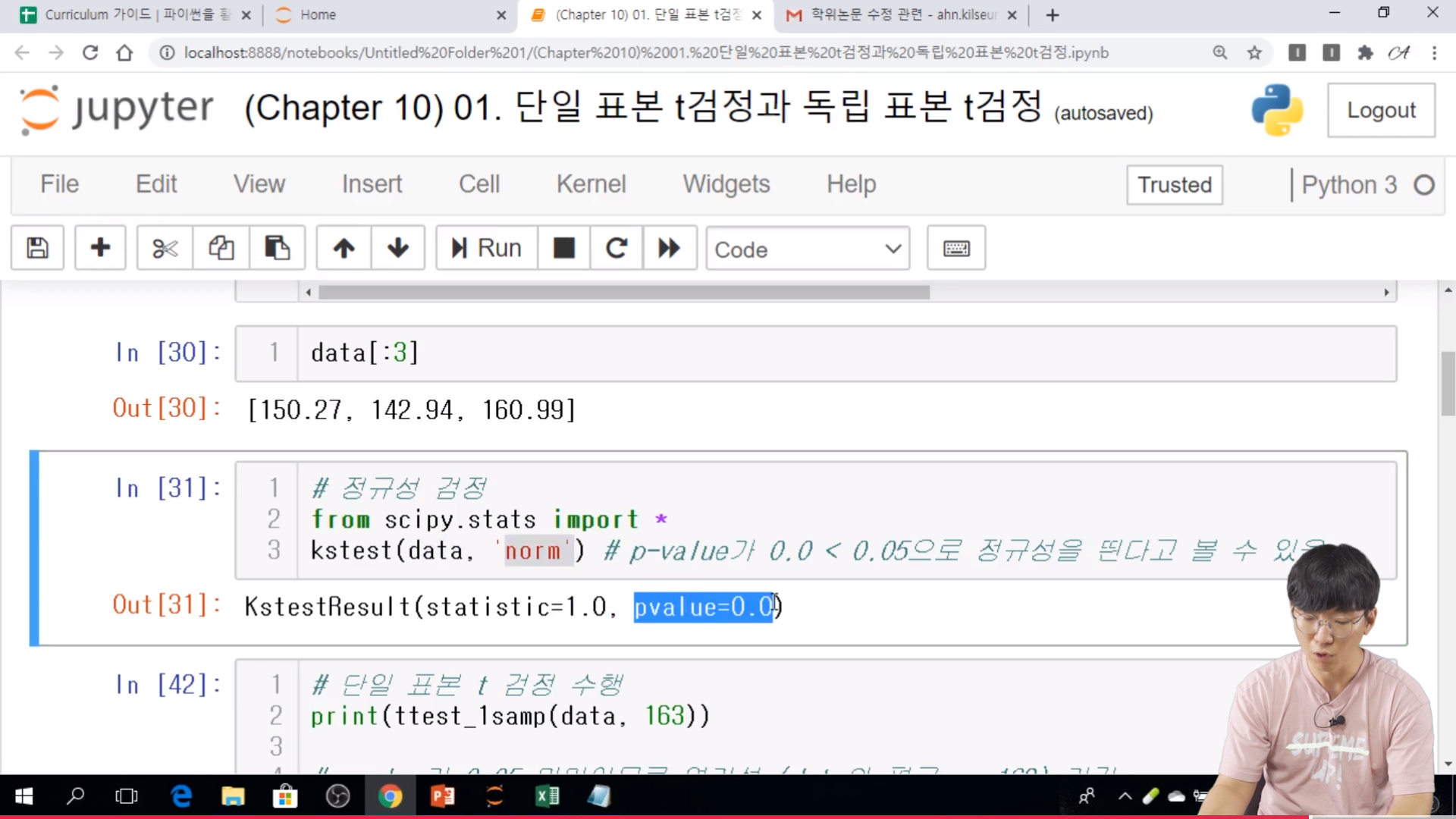
// 0.0 으로 나왔기 때문에 0.05보다 낮아서 정규성을 띈다고 볼 수 있다.
// 단일 표본 t 검정 수행
// 0.05 미만이므로 영가설은 기각되고, 통계량이 음수이므로 data 평균이 163보다 작는 것을 알 수 있다.
[02. Part 2) 탐색적 데이터 분석 Chapter 10. 둘 사이에는 무슨 관계가 있을까 - 가설 검정과 변수 간 관계 분석 - 02. 독립 표본 t 검정]
* 독립 표본 t - 검정 개요
- 목적 : 서로 다른 두 그룹의 데이터 평균 비교
// 단일 표본 t-검정 보다는 더 많이 쓰인다.
- 영 가설과 대립 가설

- 가설 수립 예시 : 2020년 7월 한 달 간 지점 A의 일별 판매량과 지점 B의 일별 판매량이 아래와 같다면, 지점 A와 지점 B의 7월 판매량 간 유의미한 차이가 있는가?

* 독립 표본 t - 검정 선행 조건
- 독립성 : 두 그룹은 서로 독립적이어야 한다.
// 한 그룹의 평균이 다른 그룹의 평균에 영향을 미치지 않아야 한다.
- 정규성 : 데이터는 정규분포를 따라야 한다.
. 정규성을 따르지 않으면 비모수 검정인 Mann-Whitney 검정을 수행해야 한다.
- 등분산성 : 두 그룹의 데이터에 대한 부산이 같아야 한다.
. Levene의 등분산 검정 : p-value 가 0.05 미만이면 분산이 다르다고 판단
. 분산이 같은지 다른지에 따라 사용하는 통계량이 달라지므로, 설정만 달리해주면 된다.
// 분산에 의해서 달라지므로 분산을 같거나 다르게 할 수 있다는 의미이다.
* 독립 표본 t - 검정 통계량
- 두 그룹의 분산이 같은 경우

- 두 그룹의 분산이 다른 경우

* 파이썬을 이용한 독립 표본 t-검정

// scipy.stats.levene documentation
docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.levene.html
scipy.stats.levene(*args, **kwds)Perform Levene test for equal variances.
The Levene test tests the null hypothesis that all input samples are from populations with equal variances. Levene’s test is an alternative to Bartlett’s test bartlett in the case where there are significant deviations from normality.
|
Parameters: ample1, sample2, ... : array_like center : {‘mean’, ‘median’, ‘trimmed’}, optional proportiontocut : float, optional |
|
Returns: p-value : float |
// scipy.stats.ttest_ind documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html
scipy.stats.ttest_ind(a, b, axis=0, equal_var=True, nan_policy='propagate')Calculate the T-test for the means of two independent samples of scores.
This is a two-sided test for the null hypothesis that 2 independent samples have identical average (expected) values. This test assumes that the populations have identical variances by default.
Parameters
a, barray_like
The arrays must have the same shape, except in the dimension corresponding to axis (the first, by default).
axisint or None, optional
Axis along which to compute test. If None, compute over the whole arrays, a, and b.
equal_varbool, optional
If True (default), perform a standard independent 2 sample test that assumes equal population variances [1]. If False, perform Welch’s t-test, which does not assume equal population variance [2].
New in version 0.11.0.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
Returns
statisticfloat or array
The calculated t-statistic.
pvaluefloat or array
The two-tailed p-value.
// scipy.stats.mannwhitneyu documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.mannwhitneyu.html
scipy.stats.mannwhitneyu(x, y, use_continuity=True, alternative=None)Compute the Mann-Whitney rank test on samples x and y.
Parameters
x, yarray_like
Array of samples, should be one-dimensional.
use_continuitybool, optional
Whether a continuity correction (1/2.) should be taken into account. Default is True.
alternative{None, ‘two-sided’, ‘less’, ‘greater’}, optional
Defines the alternative hypothesis. The following options are available (default is None):
None: computes p-value half the size of the ‘two-sided’ p-value and a different U statistic. The default behavior is not the same as using ‘less’ or ‘greater’; it only exists for backward compatibility and is deprecated.
‘two-sided’
‘less’: one-sided
‘greater’: one-sided
Use of the None option is deprecated.
Returns
statisticfloat
The Mann-Whitney U statistic, equal to min(U for x, U for y) if alternative is equal to None (deprecated; exists for backward compatibility), and U for y otherwise.
pvaluefloat
p-value assuming an asymptotic normal distribution. One-sided or two-sided, depending on the choice of alternative.
* 실습

// scipy 에서는 Series 보다는 ndarray 가 더 낮기 때문에 values 를 만들어서 들고 있다.
// 만약에 NaN 값이 있다면 float 형태로 나오기 때문에 수치에서 .0 으로 나온다면 NaN 이 있다는 것을 알 고 있어야 한다.
[02. Part 2) 탐색적 데이터 분석 Chapter 10. 둘 사이에는 무슨 관계가 있을까 - 가설 검정과 변수 간 관계 분석 - 03. 쌍체 표본 t 검정]

* 쌍체 표본 t - 검정 개요
- 목적 : 특정 실험 및 조치 등의 효과가 유의한지를 확인

// n 가 있으면 동일한 n 가 있어야 한다.
* 쌍체 표본 t - 검정의 선행 조건
- 실험 전과 후의 측정 값 (즉, X 와 Y)은 정규 분포를 따르지 않아도 무방하다.
- 그러나 측정 값의 차이인 d는 정규성을 갖고 있어야 한다.
* 쌍체 표본 t - 검정의 통계량

* 파이썬을 이용한 쌍체 표본 t - 검정
// scipy.stats.ttest_rel documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html
scipy.stats.ttest_rel(a, b, axis=0, nan_policy='propagate')Calculate the t-test on TWO RELATED samples of scores, a and b.
This is a two-sided test for the null hypothesis that 2 related or repeated samples have identical average (expected) values.
Parameters
a, barray_like
The arrays must have the same shape.
axisint or None, optional
Axis along which to compute test. If None, compute over the whole arrays, a, and b.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
Returns
statisticfloat or array
t-statistic.
pvaluefloat or array
Two-sided p-value.
* 실습
// 정규성 검정을 해줘야 한다. after - before 를 통해서 확인을 해준다.
[파이썬을 활용한 데이터 전처리 Level UP-Comment]
- 쌍체표본 t- 검정, 독립 표본 t- 검정, 단일 표본 t- 검정
파이썬을 활용한 데이터 전처리 Level UP 올인원 패키지 Online. | 패스트캠퍼스
데이터 분석에 필요한 기초 전처리부터, 데이터의 품질 및 머신러닝 성능 향상을 위한 고급 스킬까지 완전 정복하는 데이터 전처리 트레이닝 온라인 강의입니다.
www.fastcampus.co.kr
'Programming > Python' 카테고리의 다른 글
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 15회차 미션 (0) | 2020.11.16 |
|---|---|
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 14회차 미션 (0) | 2020.11.15 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 12회차 미션 (0) | 2020.11.13 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 11회차 미션 (0) | 2020.11.12 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 10회차 미션 (0) | 2020.11.11 |


