[패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 17회차 미션 Programming/Python2020. 11. 18. 11:01
[파이썬을 활용한 데이터 전처리 Level UP- 16 회차 미션 시작]
* 복습
- 군집화 및 연관 규칙 탐색 이론에 대해서 배워 보았다.
[02. Part 2) 어디서 많이 봤던 패턴이다 싶을 때 - 빈발 패턴 탐색 - 01-2. 연관 규칙 탐색(실습)]
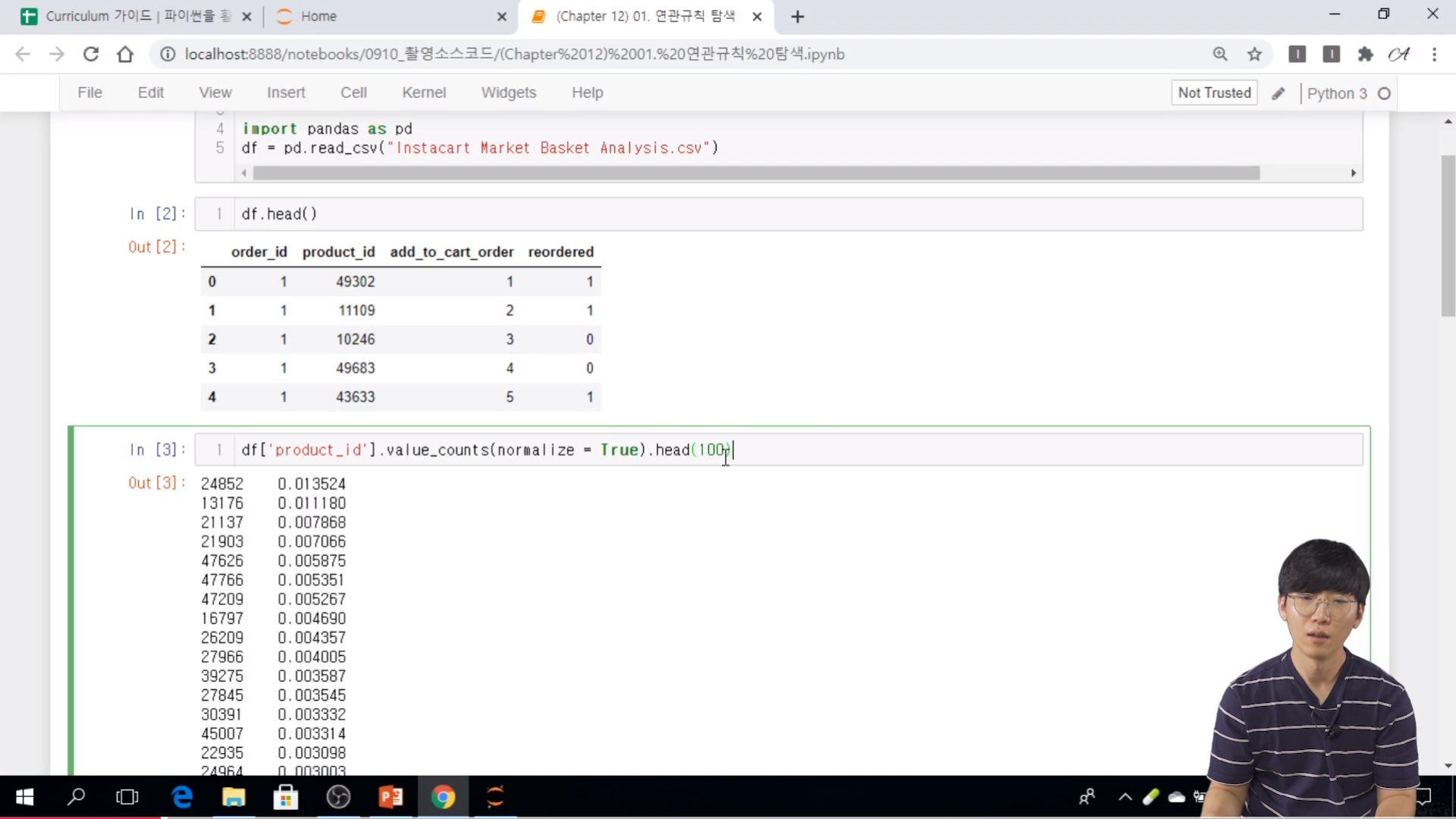
// value_counts 를 통해서 빈도를 item 에 대한 빈도를 보는 것이다.
// order_id 기준으로 product_id 를 apply(list) 를 통해서 list 형태로 정리를 하는 것이다.
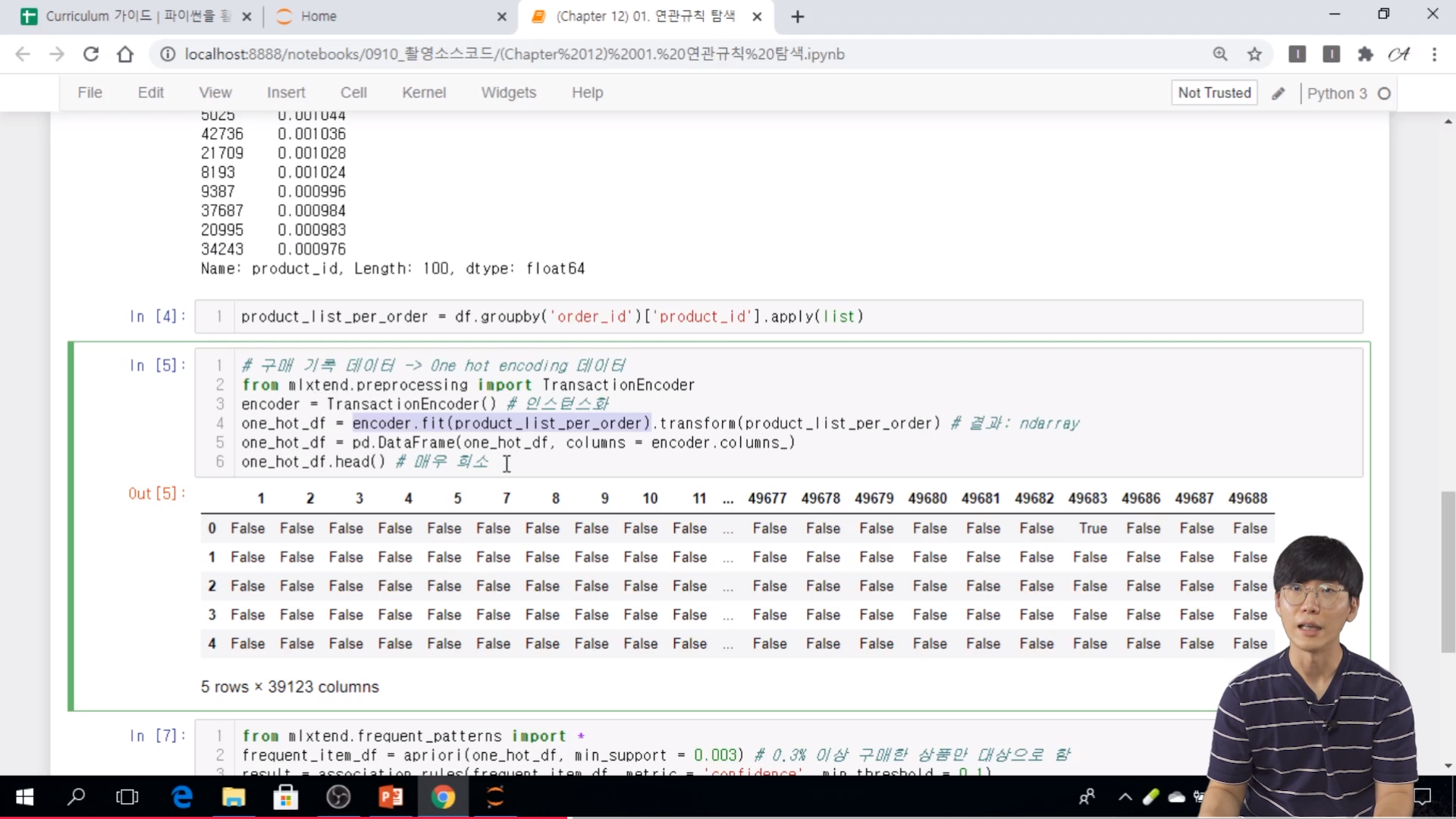
// TransactionEncoder 로 instance 를 시켜서 fit 를 학습을 시키는 것이다. 거기에 transform 을 해줘야 한다.
// 결과는 ndarray 형태로 return 이 된다. ndarrray는 분석하기가 쉽지 않기 때문에 dataframe 화 시켜서 확인한다.
// False 는 0, True 1
// 매우 희소한 데이터 형태로 나왔다. (sparse) 하다고 볼 수 있다.
// apriori 함수로 원하는 데이터를 찾아 본다. min_support = 0.003 # 0.3% 구매한 상품만 대상으로 했다. 이것 또한 흔치 않는 데이터라고 보면 된다.
[02. Part 2) 어디서 많이 봤던 패턴이다 싶을 때 - 빈발 패턴 탐색 - 02-1. 빈발 시퀀스 탐색 (이론)]

* 시퀀스 데이터란?
- 시퀀스 데이터란 각 요소가 (순서, 값) 형태로 구성된 데이터로, 분석 시에 반드시 순서를 고려해야 한다.
// 일종의 tuple, vector 형태로 된것

// 이벤트.. 즉 사건이 될 수도 있고..
- 로그 데이터 대부분이 순서가 있는 시퀀스 데이터이다.
. 고객 구매 기록
. 고격 여정
. 웹 서핑 기록
* 시퀀스 데이터에서의 빈발 패턴
- 시퀀스 데이터에서의 빈발 패턴은 반드시 순서가 고려되어야 한다.

* 지지도와 신뢰도
- 분석 목적에 따라, 특정 패턴의 등장 여부에 대한 정의가 필요하다.

- 일반적으로, 윈도우 내 (크기 L) 에 특정 이벤트가 발생했는지를 기준으로 패턴의 등장 여부를 확인
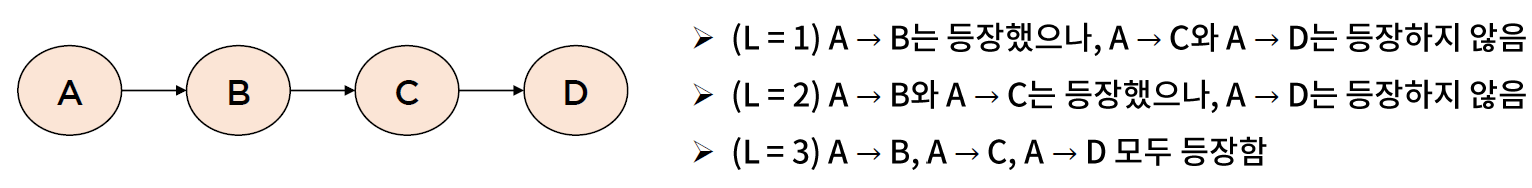
- 지지도와 신뢰도에 대한 정의는 일반 데이터에 대한 것과 같으나, 출현 횟수를 계산하는 방식이 다름
* 순서를 고려한 연관규칙 탐사
- 시퀀스 데이터에 대한 연관규칙 탐사에 대해서는 A -> B와 B -> A 가 다른 지지도를 갖기 때문에, 같은 항목 집합으로부터 규칙을 생성할 수 없다.
- 신뢰도에 대한 apriori 원리는 성립한다.
- 따라서 개별 요소(이벤트)에 다른 요소를 추가하는 방식으로 규칙을 아래와 같이 직접 찾아 나가야 한다.

// 이벤트 목록 -> 빈발 이벤트 추출 -> 추가 및 지지도 계산 -> 집합탐색 -> 규칙 만들기
// 추출은 응용을 하는 것이라고 보면 된다.
// 신뢰도가 있기 때문에 가능한 것이다.
* 동적 프로그래밍
- 원 문제를 작은 문제로 분할한 다음 점화식으로 만들어 재귀적인 형태로 원 문제를 해결하는 방식
// 동적 프로그래밍에 대해서는 좀더 조사가 필요하다.~
- 시퀀스 데이터에 대한 연관 규칙 탐사 적용을 위한 동적 프로그래밍 구조

// Dynamic Programming 관련 괜찮은 사이트
towardsdatascience.com/beginners-guide-to-dynamic-programming-8eff07195667
What is Dynamic Programming?
Dynamic programming is a terrific approach that can be applied to a class of problems for obtaining an efficient and optimal solution.
In simple words, the concept behind dynamic programming is to break the problems into sub-problems and save the result for the future so that we will not have to compute that same problem again. Further optimization of sub-problems which optimizes the overall solution is known as optimal substructure property.
Two ways in which dynamic programming can be applied:
Top-Down:
In this method, the problem is broken down and if the problem is solved already then saved value is returned, otherwise, the value of the function is memoized i.e. it will be calculated for the first time; for every other time, the stored value will be called back. Memoization is a great way for computationally expensive programs. Don’t confuse memoization with memorize.
// memoization..으로 접근
Memoize != memorize
Bottom-Up:
This is an effective way of avoiding recursion by decreasing the time complexity that recursion builds up (i.e. memory cost because of recalculation of the same values). Here, the solutions to small problems are calculated which builds up the solution to the overall problem. (You will have more clarity on this with the examples explained later in the article).
Understanding Dynamic Programming With Examples
Let’s start with a basic example of the Fibonacci series.
Fibonacci series is a sequence of numbers in such a way that each number is the sum of the two preceding ones, starting from 0 and 1.
F(n) = F(n-1) + F(n-2)
- Recursive method:
def r_fibo(n):
if n <= 1:
return n
else:
return(r_fibo(n-1) + r_fibo(n-2))Here, the program will call itself, again and again, to calculate further values. The calculation of the time complexity of the recursion based approach is around O(2^N). The space complexity of this approach is O(N) as recursion can go max to N.
For example-
F(4) = F(3) + F(2) = ((F(2) + F(1)) + F(2) = ((F(1) + F(0)) + F(1)) + (F(1) + F(0))
In this method values like F(2) are computed twice and calls for F(1) and F(0) are made multiple times. Imagine the number of repetitions if you have to calculate it F(100). This method is ineffective for large values.
- Top-Down Method
def fibo(n, memo):
if memo[n] != null:
return memo[n]
if n <= 1:
return n
else:
res = fibo(n-1) + fibo(n+1)
memo[n] = res
return resHere, the computation time is reduced significantly as the outputs produced after each recursion are stored in a list which can be reused later. This method is much more efficient than the previous one.
- Bottom down
def fib(n):
if n<=1:
return n
list_ = [0]*(n+1)
list_[0] = 0
list_[1] = 1
for i in range(2, n+1):
list_[i] = list_[i-1] + list[i-2]
return list_[n]This code doesn’t use recursion at all. Here, we create an empty list of length (n+1) and set the base case of F(0) and F(1) at index positions 0 and 1. This list is created to store the corresponding calculated values using a for loop for index values 2 up to n.
Unlike in the recursive method, the time complexity of this code is linear and takes much less time to compute the solution, as the loop runs from 2 to n, i.e., it runs in O(n). This approach is the most efficient way to write a program.
Time complexity: O(n) <<< O(2^N)
// Tablulation vs Memoization
www.geeksforgeeks.org/tabulation-vs-memoization/
There are following two different ways to store the values so that the values of a sub-problem can be reused. Here, will discuss two patterns of solving DP problem:
- Tabulation: Bottom Up
- Memoization: Top Down
Before getting to the definitions of the above two terms consider the below statements:
- Version 1: I will study the theory of Dynamic Programming from GeeksforGeeks, then I will practice some problems on classic DP and hence I will master Dynamic Programming.
- Version 2: To Master Dynamic Programming, I would have to practice Dynamic problems and to practice problems – Firstly, I would have to study some theory of Dynamic Programming from GeeksforGeeks
Both the above versions say the same thing, just the difference lies in the way of conveying the message and that’s exactly what Bottom Up and Top Down DP do. Version 1 can be related to as Bottom Up DP and Version-2 can be related as Top Down Dp.
Tabulation Method – Bottom Up Dynamic Programming
As the name itself suggests starting from the bottom and cumulating answers to the top. Let’s discuss in terms of state transition.
Let’s describe a state for our DP problem to be dp[x] with dp[0] as base state and dp[n] as our destination state. So, we need to find the value of destination state i.e dp[n].
If we start our transition from our base state i.e dp[0] and follow our state transition relation to reach our destination state dp[n], we call it Bottom Up approach as it is quite clear that we started our transition from the bottom base state and reached the top most desired state.
Now, Why do we call it tabulation method?
To know this let’s first write some code to calculate the factorial of a number using bottom up approach. Once, again as our general procedure to solve a DP we first define a state. In this case, we define a state as dp[x], where dp[x] is to find the factorial of x.
Now, it is quite obvious that dp[x+1] = dp[x] * (x+1)
// Tabulated version to find factorial x. int dp[MAXN]; // base case int dp[0] = 1; for (int i = 1; i< =n; i++) { dp[i] = dp[i-1] * i; }
The above code clearly follows the bottom-up approach as it starts its transition from the bottom-most base case dp[0] and reaches its destination state dp[n]. Here, we may notice that the dp table is being populated sequentially and we are directly accessing the calculated states from the table itself and hence, we call it tabulation method.
Memoization Method – Top Down Dynamic Programming
Once, again let’s describe it in terms of state transition. If we need to find the value for some state say dp[n] and instead of starting from the base state that i.e dp[0] we ask our answer from the states that can reach the destination state dp[n] following the state transition relation, then it is the top-down fashion of DP.
Here, we start our journey from the top most destination state and compute its answer by taking in count the values of states that can reach the destination state, till we reach the bottom most base state.
Once again, let’s write the code for the factorial problem in the top-down fashion
// Memoized version to find factorial x. // To speed up we store the values // of calculated states // initialized to -1 int dp[MAXN] // return fact x! int solve(int x) { if (x==0) return 1; if (dp[x]!=-1) return dp[x]; return (dp[x] = x * solve(x-1)); }
As we can see we are storing the most recent cache up to a limit so that if next time we got a call from the same state we simply return it from the memory. So, this is why we call it memoization as we are storing the most recent state values.
In this case the memory layout is linear that’s why it may seem that the memory is being filled in a sequential manner like the tabulation method, but you may consider any other top down DP having 2D memory layout like Min Cost Path, here the memory is not filled in a sequential manner.

This article is contributed by Nitish Kumar. If you like GeeksforGeeks and would like to contribute, you can also write an article using or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
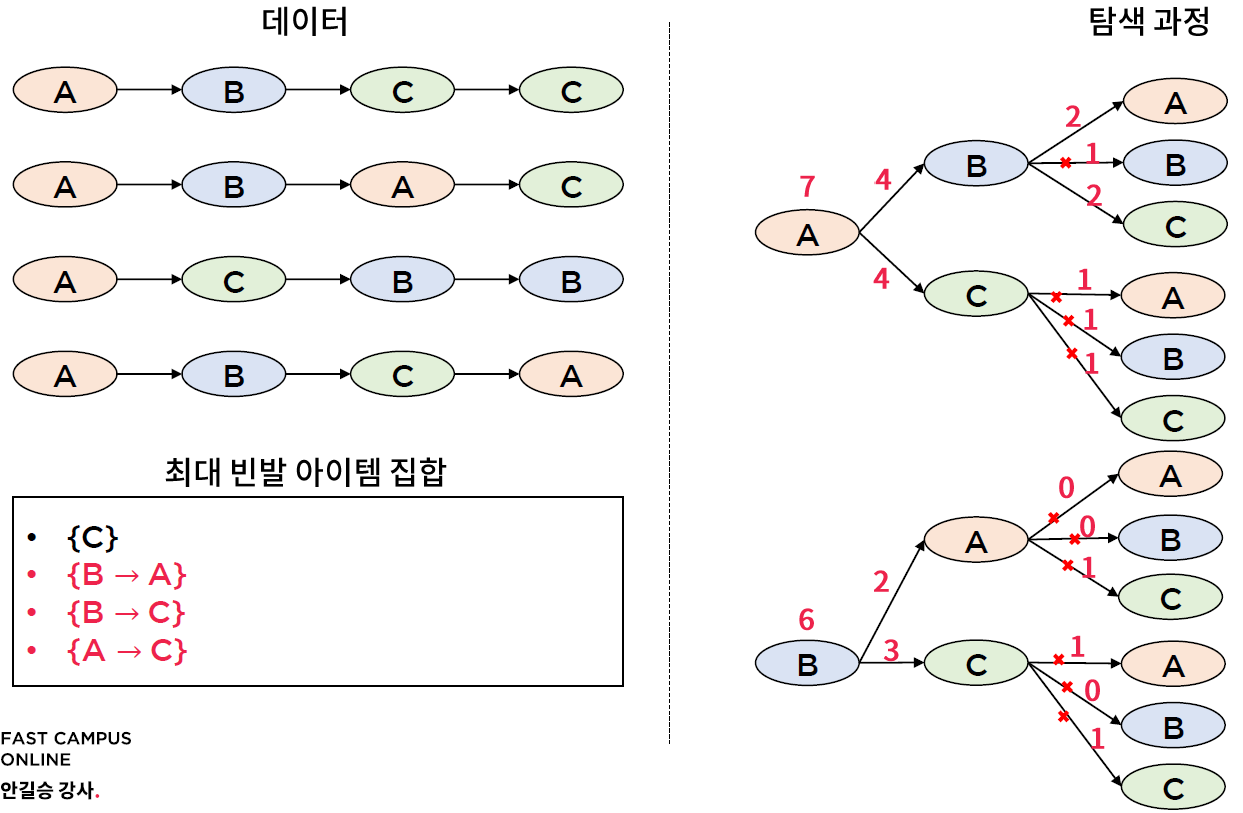
* 순서를 고려한 연관규칙 탐사 (예시 : L = 2, 최소 지지도 = 2)


* 순서를 고려한 연관규칙 탐사 (예시 : L = 2, 최소 지지도 = 3)


[02. Part 2) 어디서 많이 봤던 패턴이다 싶을 때 - 빈발 패턴 탐색 - 02-2. 빈발 시퀀스 탐색 (실습)]

// 만약에 순서가 없으면 순서를 만들면 된다.
// 순서가 중요한 데이터이기 때문에 고객ID, 순서를 정리를 해줘야 한다.
// unique () 찾아보기
// itertools.product() 함수에 대해서 알아보기
// pattern에 포함된 모든 아이템 집합이 recor에 포함된 아이템 집합에 속하지 않는지 체크
// 순서가 있기 때문에 반드시 존재했다고 볼 순 없다.
// 가능한 모든 조합에서 위치 간거리가 L이하면 True 를 반환
// find_maximum_frequent_sequence_item 함수를 만든다.
// 만들어진 함수들을 이용해서 원하는 프로젝트등에 활용해서 사용하면 된다.
// pandas.unique Documentation
pandas.pydata.org/pandas-docs/stable/reference/api/pandas.unique.html
pandas.unique(values)Hash table-based unique. Uniques are returned in order of appearance. This does NOT sort.
Significantly faster than numpy.unique. Includes NA values.
Parametersvalues1d array-likeReturnsnumpy.ndarray or ExtensionArray
The return can be:
-
Index : when the input is an Index
-
Categorical : when the input is a Categorical dtype
-
ndarray : when the input is a Series/ndarray
Return numpy.ndarray or ExtensionArray.
The return can be:
-
Index : when the input is an Index
-
Categorical : when the input is a Categorical dtype
-
ndarray : when the input is a Series/ndarray
Return numpy.ndarray or ExtensionArray.
Return unique values from an Index.
Return unique values of Series object.
// itertools.product Documentation
docs.python.org/3/library/itertools.html#itertools.product
itertools.product(*iterables, repeat=1)Cartesian product of input iterables.
Roughly equivalent to nested for-loops in a generator expression. For example, product(A, B) returns the same as ((x,y) for x in A for y in B).
The nested loops cycle like an odometer with the rightmost element advancing on every iteration. This pattern creates a lexicographic ordering so that if the input’s iterables are sorted, the product tuples are emitted in sorted order.
To compute the product of an iterable with itself, specify the number of repetitions with the optional repeat keyword argument. For example, product(A, repeat=4) means the same as product(A, A, A, A).
This function is roughly equivalent to the following code, except that the actual implementation does not build up intermediate results in memory:
def product(*args, repeat=1):
# product('ABCD', 'xy') --> Ax Ay Bx By Cx Cy Dx Dy
# product(range(2), repeat=3) --> 000 001 010 011 100 101 110 111
pools = [tuple(pool) for pool in args] * repeat
result = [[]]
for pool in pools:
result = [x+[y] for x in result for y in pool]
for prod in result:
yield tuple(prod)Before product() runs, it completely consumes the input iterables, keeping pools of values in memory to generate the products. Accordingly, it only useful with finite inputs.
[파이썬을 활용한 데이터 전처리 Level UP-Comment]
- 빈발 개념에 대해서 배웠으나 약간의 개념 정리가 필요한 것 같다. 어떤 sequence 를 이뤄서 나타내는 조건들에 대해서 분석을 해보고, 어똔 조건에서 어떠한 결과물을 내놓는 것에 대해서는 좀 더 연구가 필요하지 않나 싶다.
파이썬을 활용한 데이터 전처리 Level UP 올인원 패키지 Online. | 패스트캠퍼스
데이터 분석에 필요한 기초 전처리부터, 데이터의 품질 및 머신러닝 성능 향상을 위한 고급 스킬까지 완전 정복하는 데이터 전처리 트레이닝 온라인 강의입니다.
www.fastcampus.co.kr
'Programming > Python' 카테고리의 다른 글
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 19회차 미션 (0) | 2020.11.20 |
|---|---|
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 18회차 미션 (0) | 2020.11.19 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 16회차 미션 (0) | 2020.11.17 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 15회차 미션 (0) | 2020.11.16 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 14회차 미션 (0) | 2020.11.15 |


